
Scipy介绍
Scipy是一个用于数学、科学、工程领域的常用软件包,可以处理插值、积分、优化、常微分方程数值解的求解、图像处理、信号处理等问题。它用于有效计算Numpy矩阵,使Numpy和Scipy协同工作,高效解决问题。
Scipy特点
Scipy支持大多数工程数学运算。
Scipy每一个子模块都可以完成一类功能。
Scipy中的函数类似于MATLAB中的函数,使用方便。
Scipy应用
Scipy常数模块
1 | from scipy import constants as C |
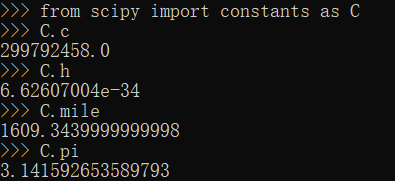
Scipy特殊函数模块
gamma,gammaln方法
1 | from scipy import special as S |
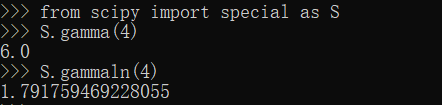
log1p方法
1 | from scipy import special as S |
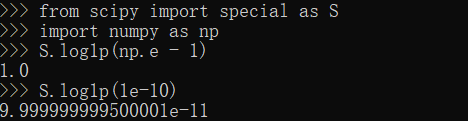
Scipy拟合优化模块
fsolve方法
1 | from scipy import optimize as O |
$$ \begin{cases} 5x_1 + 3 & = 0 \\ 4{x_0}^2 -2\sin(x_1 \cdot x_2) & = 0 \\ x_1 \cdot x_2 -1.5 &= 0 \end{cases} $$
leastsq方法
1 | from scipy import optimize as O |
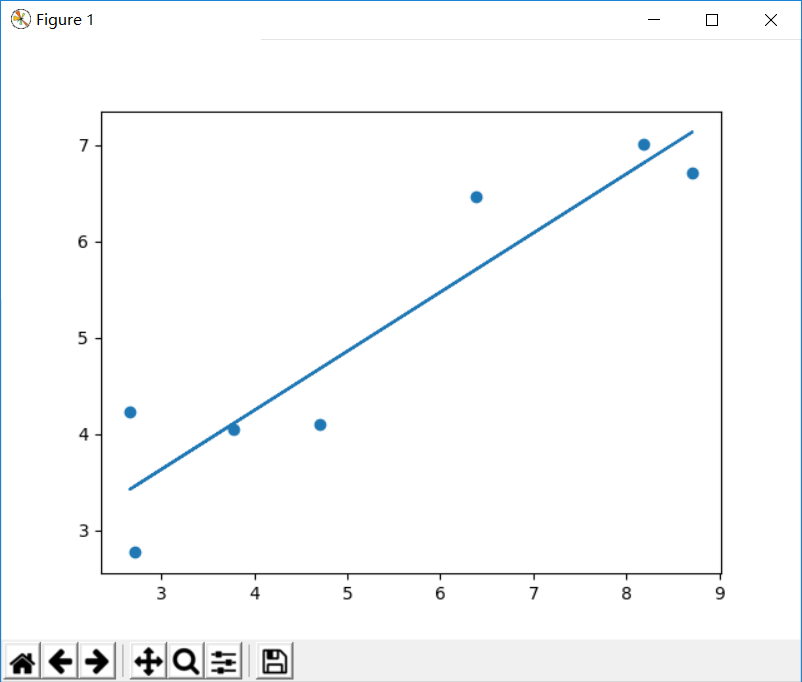
Scipy线性代数模块
solve方法
1 | from scipy import linalg as L |
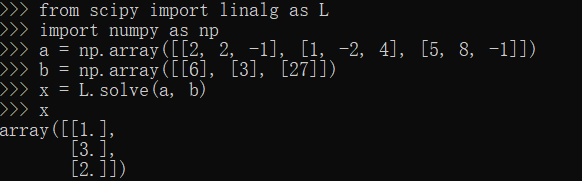
eig,svd方法
1 | from scipy import linalg as L |
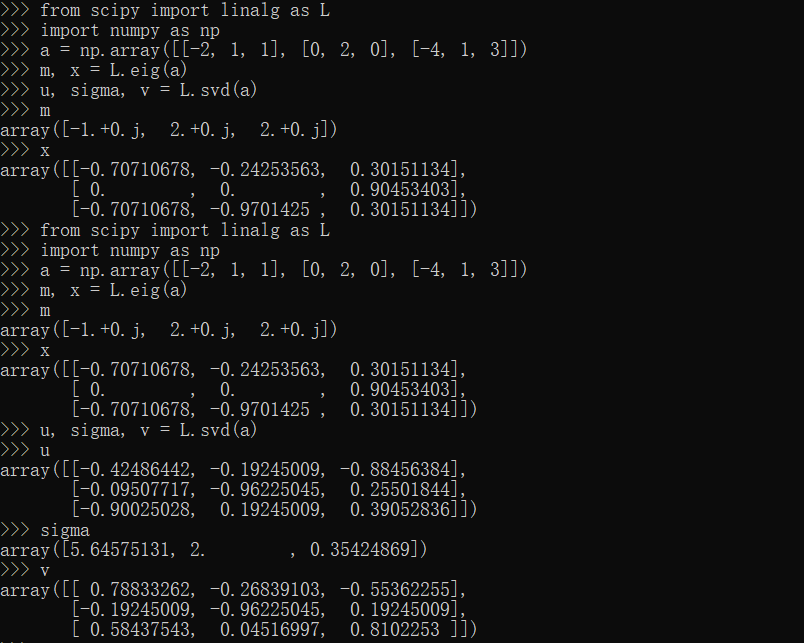
Scipy统计模块
norm类,stats,rvs方法
1 | from scipy import stats as ST |
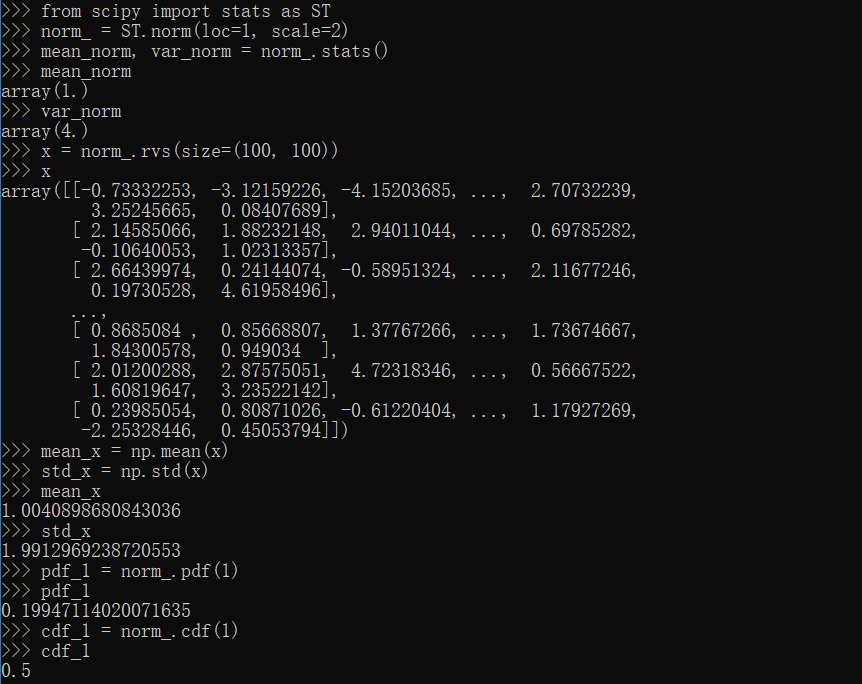
rv_discrete类,stats,rvs方法
1 | from scipy import stats as ST |
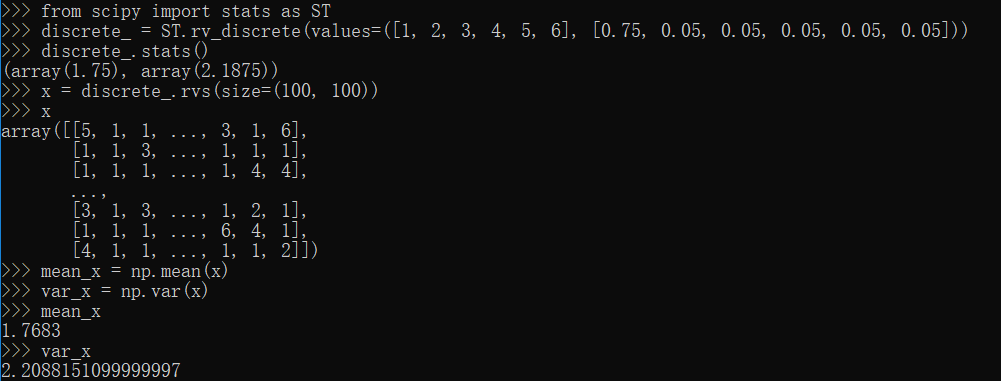
binom.pmf方法
1 | from scipy import stats as ST |

Scipy积分模块
quad方法
1 | from scipy import integrate as I |
$$\int_{-1}^{1} \sqrt{1-x^2}, dx = \frac{\pi}{2}$$
dblquad,tplquad方法
1 | from scipy import integrate as I |
$$\int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \sqrt{1-x^2-y^2}, dydx = \frac{2}{3}\pi$$
Scipy插值模块
interp1d,interp2d方法
1 | from scipy import interpolate as IP |
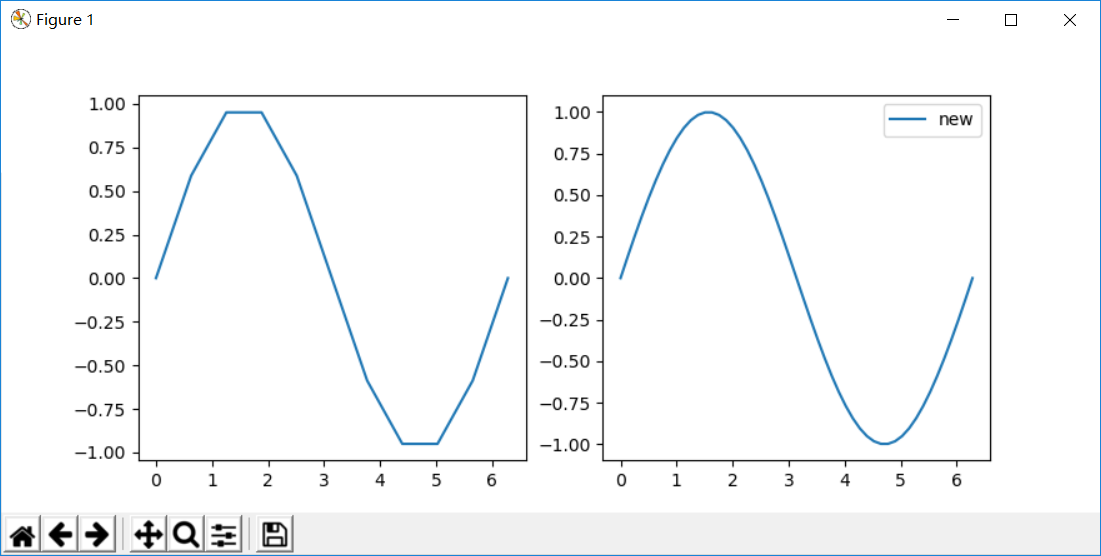
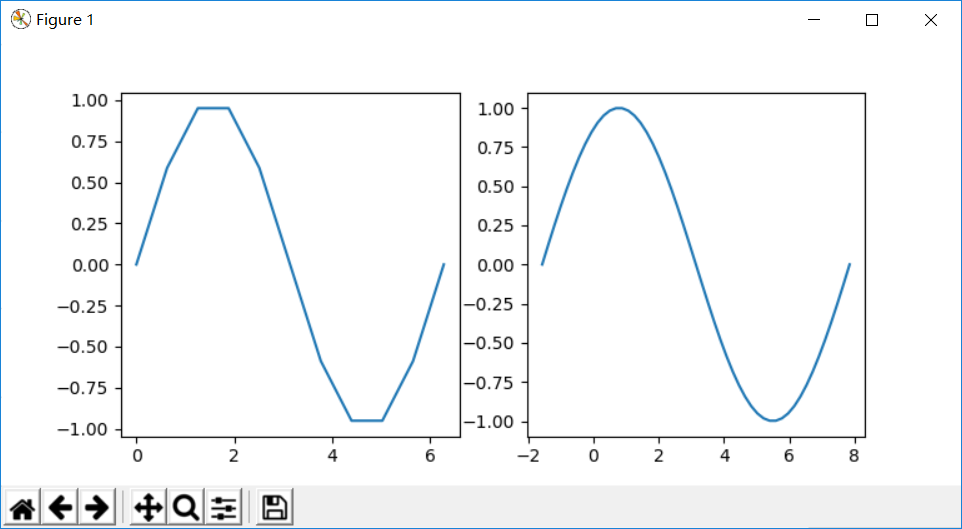
UnivariateSpline方法
1 | from scipy import interpolate as IP |
Scipy信号处理模块
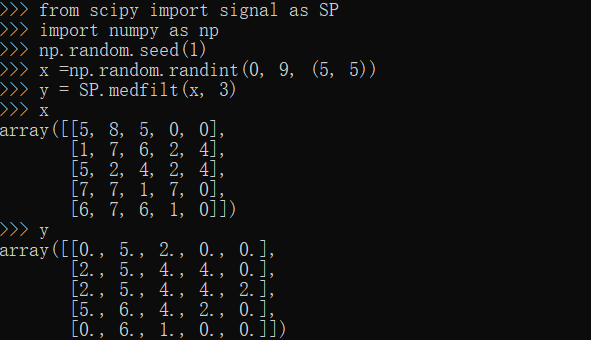
medfilt方法
1 | from scipy import signal as SP |
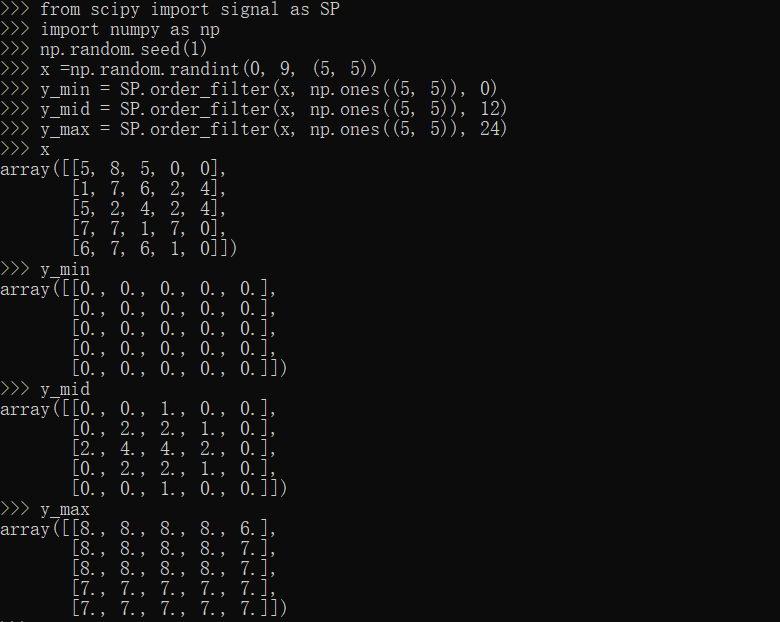
order_filter方法
1 | from scipy import signal as SP |
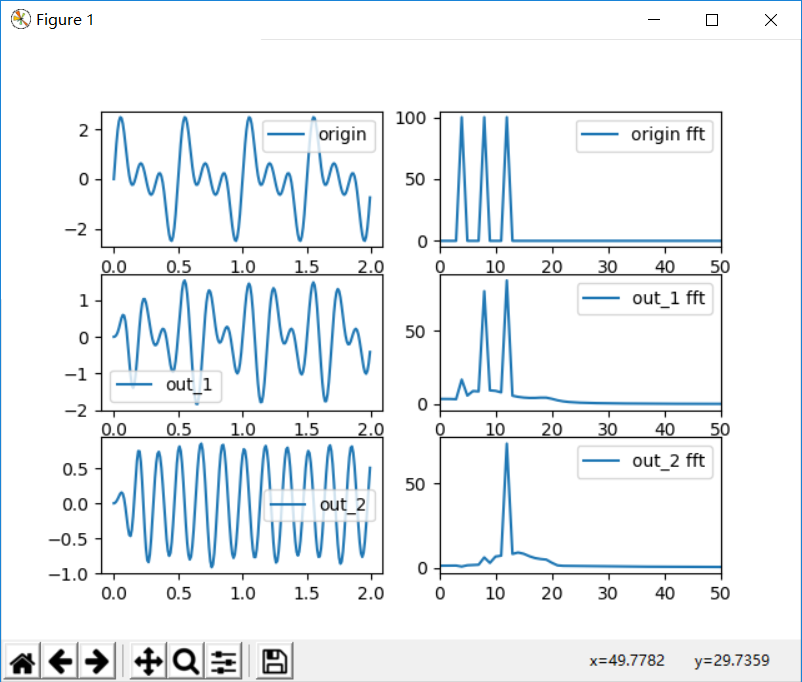
iirdesign,lfilter方法
1 | from scipy import signal as SP |
Scipy图像处理模块
Scipy.ndimage 是一个处理多维图像的函数库,其中又包括以下模块。
filters 图像滤波器函数库
fourier 傅里叶变换函数库
interpolation 图像变换函数库
morphology 形态学操作函数库
图像处理有许多更强大的库,如opencv,scikit-image库,在此不做过多介绍,可以参考opencv。
Scipy小结
通过Scipy,使用者可以仅需要几行代码,便可以完成一系列工程应用。在数据分析,实际项目中,常常需要对数据进行插值、拟合、优化,需要借助Scipy科学计算库的帮助,因此Scipy是工程研究中必不可少的帮手。